同時分布と条件付き分布
\(X\) と\(Y\) を2つの確率変数とおく。この2つの確率変数の組\((X, Y)\) を確率変数ベクトルと呼び、 \((X, Y)\) が同時に発生する事象を考える。\(X\) 、100円玉のコイントスの実現値を\(Y\) として、\(\mathbb{R}^2\) (これは二次元の実数の集合を意味する)に属する要素の上で定義される。
同時分布と周辺分布の理論
同時分布について、まず離散確率変数を考える。\((X,Y)\) に関する具体的な値が一緒に与えられることを意味する。\[
p(x, y) = P(X = x, Y = y)
\] で与えられるし、累積分布関数は \[
F(x, y) = P(X \leq x, Y \leq y)
\] で定義できる。基本は1次元確率分布と同様に定義できる。[久保川] 、最初から一般の\(d\) 次元確率変数の分布について定義をして、 \(d=1\) や\(d=2\) のときを特別な場合として記述しているような書籍もある[清水] 。
\(X\) の周辺分布は、同時に起こりうる\(Y\) の値すべてを考慮したときの確率で、
\[
F_X(x) = P(X \leq x, Y \leq \infty)=\sum_{x \in X}^x\sum_{y \in Y}^{\infty}p(x, y)
\]
クロス表と同時分布
もっと気楽に考えるとクロス集計表は同時分布の離散表現に近い。同時 周辺分布である。これがわかるとまあまあ集計時の見通しが良くなると思うし、
同時分布と周辺分布の可視化
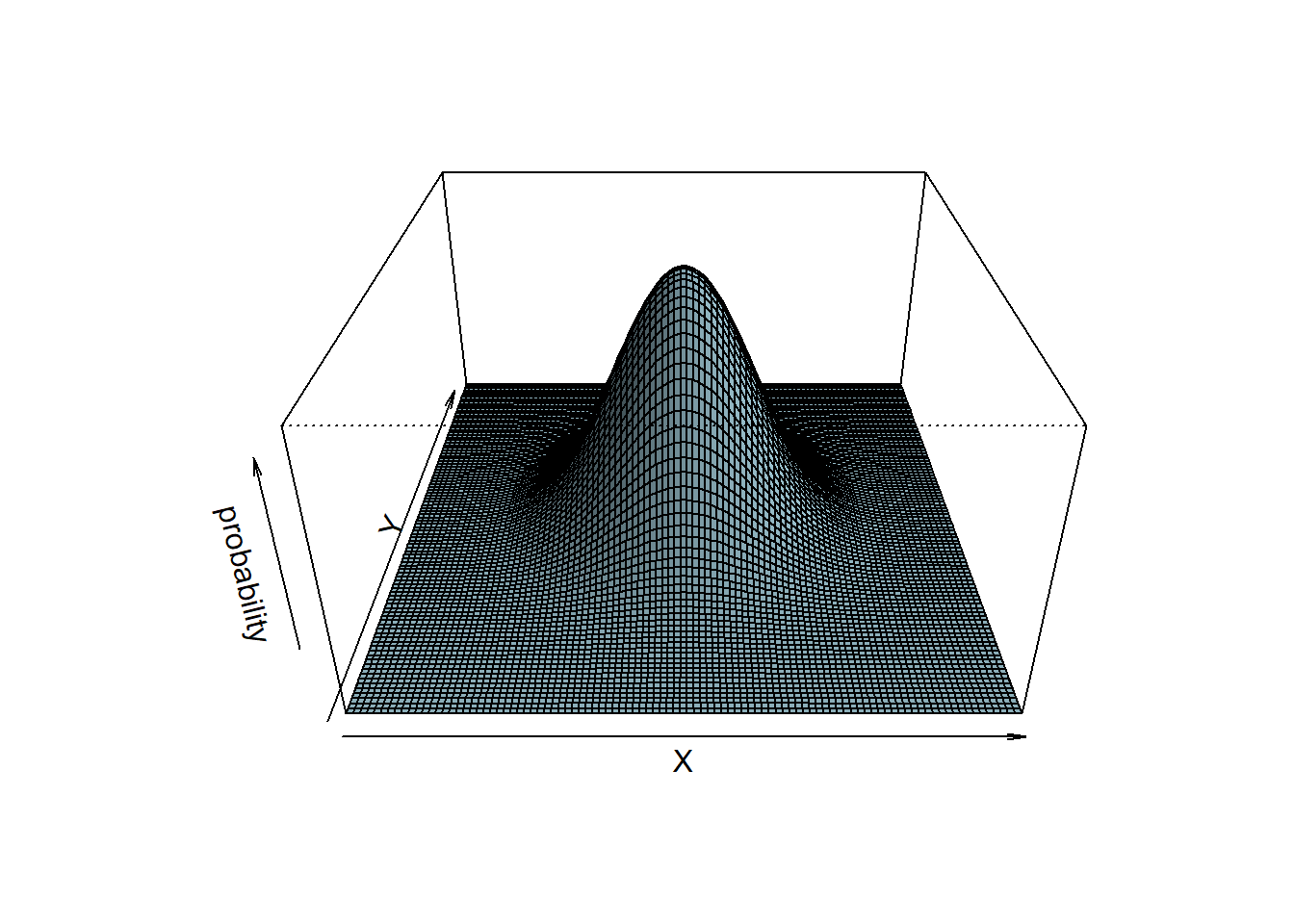
ChatGPTに「同時分布のようなグラフを描くRのコードを描いて!」ってお願いしてみる。
# define density mixture function <- function (x, y, mu = 0 , sigma = 1 ) {<- dnorm (x, mean = mu, sd = sigma) * dnorm (y, mean = mu, sd = sigma)# code below was written by ChatGPT # Create a grid of x and y values <- seq (- 4 , 4 , length.out = 100 )<- seq (- 4 , 4 , length.out = 100 )<- outer (x, y, dens_mixture)# Create the 3D plot persp (x, y, z,a = 30 , phi = 30 , expand = 0.5 ,col = "lightblue" , ltheta = 120 , shade = 0.3 ,xlab = "X" , ylab = "Y" , zlab = "probability"
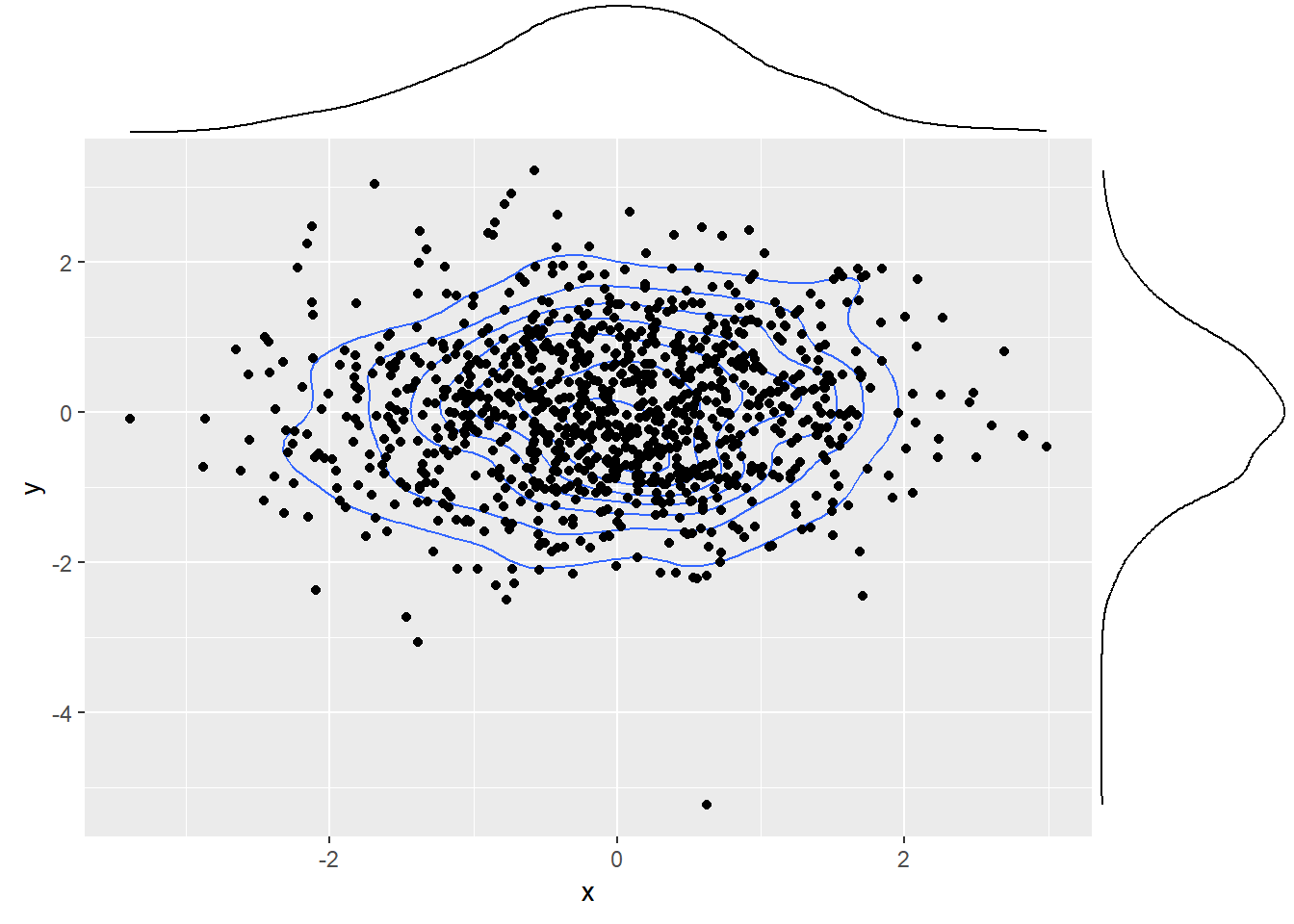
周辺分布は、例えば以下。上と右にあるのが周辺分布。
# Load the necessary libraries set.seed (523 )library (ggplot2)library (ggExtra)# define density mixture function <- function (x, y, mu = 0 , sigma = 1 ) {<- dnorm (x, mean = mu, sd = sigma) * dnorm (y, mean = mu, sd = sigma)# Define the normal distribution parameters <- 0 <- 1 # Create a dataset with x and y values <- rnorm (1000 , mu, sigma)<- rnorm (1000 , mu, sigma)<- data.frame (x = x, y = y)# Create the 2D plot with marginal distributions <- ggplot2:: ggplot (df) + :: geom_density2d (aes (x = x, y = y), geom = "line" ) + :: geom_point (aes (x = x, y = y)) + :: scale_fill_gradient (low = "white" , high = "blue" )
Warning in ggplot2::geom_density2d(aes(x = x, y = y), geom = "line"): Ignoring
unknown parameters: `geom`
:: ggMarginal (p, type = "density" )
条件付き分布
条件付き分布は、\((X, Y)\) のうち、どちらか一方が与えられたという状態で、
\(X=x\) が与えられたときの\(Y\) の条件付き確率は以下のように記述される。
\[
P(Y=y|X=x) = \frac{P(X=x, Y=y)}{P(X=x)} = \frac{P(X=x, Y=y)}{\sum_{y \in Y}p(x, y)}
\]
あるいは以下のほうが使いやすいかも
\[
P(X=x, Y=y) = P(Y=y|X=x)P(X=x)
\]
もっというと、ここからベイズの定理が出てくる
\[
P(Y=y|X=x) = \frac{P(X=x|Y=y)P(Y=y)}{P(X=x)}
\]
解釈すると、同時分布を周辺分布で割る、ということになる。
Y=0
\(P(X=0,Y=0)\) \(P(X=1,Y=0)\) \(P(Y=0)\)
Y=1
\(P(X=0,Y=1)\) \(P(X=1,Y=1)\) \(P(Y=1)\)
Xの周辺分布
\(P(X=0)\) \(P(X=1)\) \(1\)
\(X\) と\(Y\) が互いに独立であるとは、お互いの条件付き確率がもう一方に依存しないこと。\(P(Y=y|X=x) = P(Y=y)\) が保証されること。 \[
P(X=x, Y=y) = P(Y=y)P(X=x)
\]
ここまでなんとなく離散でやってきたけど基本的には連続化するアプローチは\(\Delta x\) を用いて、
連続値における条件付き密度関数は、測度論的には注意が必要らしいけど、
この条件付き密度関数の定義は直観的には正しいものであるが、測度論的には実はより\(X\) が連続な\(x\) について\(X=x\) という事象の確率は0であるから、条件付き密度関数が どのような意味で定義できるかが明らかではないからである。
条件付き独立
条件付き独立はよく因果推論、及び因果探索で議論される事が多い気がする。\(X\) 、\(Y\) 、\(Z\) があり、\(Z=z\) が与えられたときに、\(X\) と\(Y\) が条件付き独立であるとは、 \[
f_{X,Y|Z=z}(X,Y) = f_{X|Z=z}(x)f_{Y|Z=z}(y)
\]
を満たすことをいう。
条件付き独立の応用場面について
主に統計的因果推論、統計的因果探索に応用される。因果推論の用語を整理する② -識別性の条件-
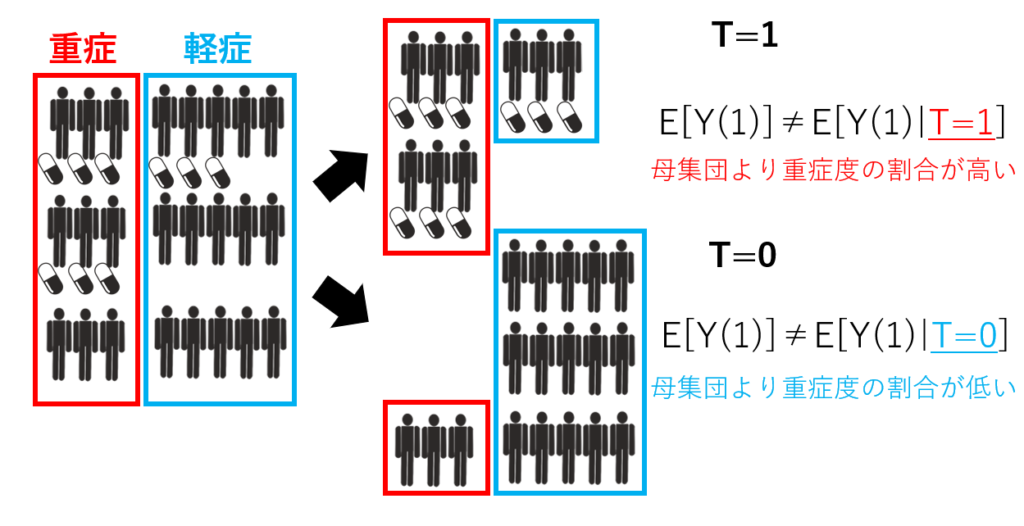
RCTにおける因果推論でよくあるのはセレクションバイアス。
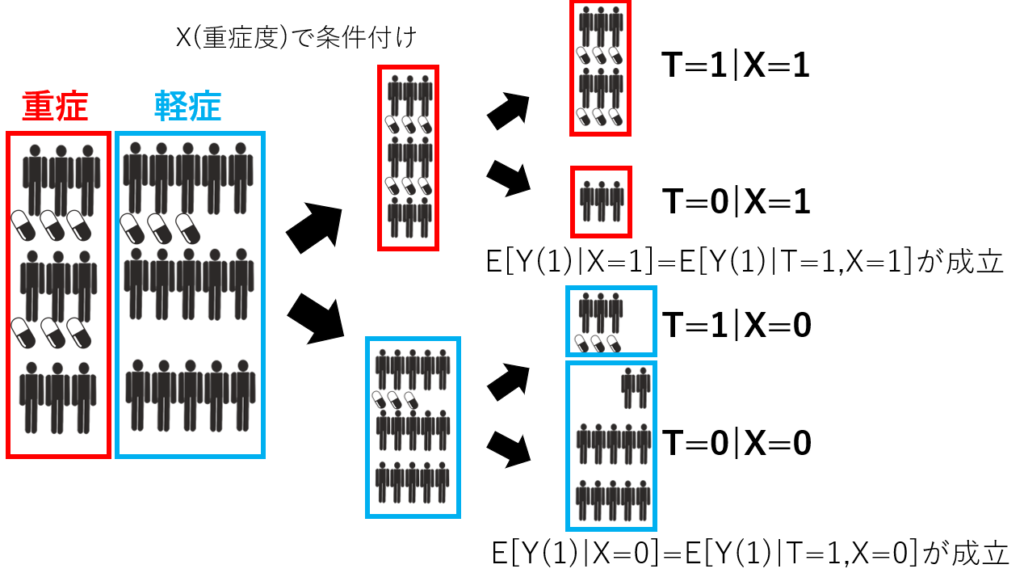
ここでは処置の有無を\(T\) 、薬効を\(Y\) 、重症度を\(X\) とおいたときに、\(X\) を条件づけた上で、 \(T\) と\(Y\) が独立であることが保証できれば、因果効果を良く推定できると保証できそう。\(X\) は1つでなくてもよく、複数あっても良い。ロジスティック回帰を使った傾向スコア法は、
ヤコビアンと畳み込み
多次元の連続確率変数を扱うとき、確率変数の変換と、それに連動する(事がある)
準備
\(X = (X_1,X_2, ..., X_n)\) を\(n\) 次元の確率変数 ベクトルとし(竹村本では「確率ベクトル」)、\(f_X(x)\) とする。この確率変数ベクトルに変換\(g\) を噛ませて、その結果を\(Y\) 、\(Y = g(X) = (g_1(x), g_2(x), ..., g_n(x))\) として考える。\(g\) にはいくつか設定がある。
すべての\(i=1,2,...,n\) に対して\(g_i(x)\) は連続微分可能
すべての\(x \in X\) に対し、\(g(X)\) が1対1対応
連続微分可能な逆関数\(g^{-1}(y)\) が存在する
逆関数の存在条件とその証明については一旦議論を省く。
解きたい問題は、\(X\) の密度関数がわかっているとき、どうやって\(Y\) の分布関数を求めようか?ということ。
ヤコビ行列
自然言語でいえば、「\(x\) の各要素を\(y\) の各要素で偏微分したときの偏微分係数を成分にした行列」で、J acobi にちなんだ\(J\) で表現されることが多い。 \(x = g^{-1}(y) = h(y)\) と置いたときに、
\[\begin{equation}
J(\frac{\partial{x}}{\partial{y}})=
\left(
\begin{matrix}
\frac{\partial{h_1(y)}}{\partial{y_1}} & ... &
\frac{\partial{h_n(y)}}{\partial{y_1}} \\
\vdots & \ddots & \vdots \\
\frac{\partial{h_1(y)}}{\partial{y_n}} & ... &
\frac{\partial{h_n(y)}}{\partial{y_n}} \\
\end{matrix}
\right)
\end{equation}\]
というような行列\(J\) をヤコビ行列(あるいは関数行列)と呼ぶことが多い。
ヤコビ行列の特殊なパターンが勾配ベクトルという考え方は別段間違いではない。\(f(x_1, x_2, ..., x_n)\) を各\(x_i\) で微分したものを並べたベクトルなので、
参考: ヤコビ行列?勾配(grad)?
ヤコビアン
ヤコビアンとして表現されるのはヤコビ行列の行列式のことである。
ヤコビ行列の行列式を\(det(J)\) とおくと、\(Y\) の密度関数は
\[
f_Y(y) = f_X(g^{-1}(y))|det(\frac{\partial{x}}{\partial{y}})| = \\
f_X(x)|\frac{\partial{x}}{\partial{y}}|
\]
と書ける。ややこしい書き方をしているが「元の確率変数の密度関数になんぼか重みをつけてスケールを揃えよう」という雰囲気を感じてくれれば、そこまでお気持ちとして理解不能な変換ではないように思う。
問題はこの変換によってえられた密度関数\(f_Y(y)\) がちゃんと確率密度関数になっているんだろうか?
畳み込み
畳み込みによる確率分布の導出は統計検定だとだいぶお作法と化している事が多い。\(X\) と\(Y\) を、密度関数が\(f_X(x)\) 、\(g_Y(y)\) で与えられる独立な確率変数とする。\(Z = X + Y\) という変数変換を行ったときの密度関数を\(f\) と\(g\) で表現することを考える。\(W = X\) とおいて、変換を整理すると
\[\begin{equation}
\left\{\,
\begin{aligned}
X = W \\
Y = Z - W
\end{aligned}
\right .
\end{equation}\]
と変換できる(逆関数)。ヤコビ行列を計算すると
\[\begin{equation}
\left(
\begin{matrix}
\frac{\partial{x}}{\partial{w}} & \frac{\partial{x}}{\partial{z}} \\
\frac{\partial{y}}{\partial{w}} & \frac{\partial{y}}{\partial{z}}
\end{matrix}
\right)
=
\left(
\begin{matrix}
1 & 0 \\
-1 & 1
\end{matrix}
\right)
\end{equation}\] で、ヤコビアンが1になる。ここが、嬉しい。
よって、\(W\) と\(Z\) の同時分布が\(f(w)g(z-w)(×1)\) ということがわかる(独立)ので、\(w\) について積分すれば、\(z\) の密度関数を算出できる。
もちろん、非線形な変換を与えたりすると、ヤコビアンは1にはならないので、
これの良いところは、分布関数がわかっていれば積分で計算ができること。\(X\) と\(Y\) がそれぞれ独立であれば、同じ分布でなくても問題はない。
正規化定数の算出
ガンマ分布とベータ分布は次回でお願い。
(標準)正規分布
正規分布の正規化定数は\(1 / \sqrt(2\pi)\) として表されるが、\(\pi\) が出てきたんだ!?」と思うことが多い。
標準正規分布の密度関数はもう覚えていると思うが以下である。
\[
f(x) = \frac{1}{\sqrt{2\pi}}\exp{\{-\frac{x^2}{2}\}}
\]
この\(\frac{1}{\sqrt{2\pi}}\) を導出する。
\(\frac{1}{c} = \int \exp{\{ - \frac{x^2}{2}\}}dx\) とおいて、\(X\) と\(Y\) がそれぞれ独立に \(c\exp{\{ - \frac{x^2}{2}\}}\) に従う確率変数とする。テクニックとしては極座標変換を行う。\((X, Y)\) を以下の通りに極座標表示し、\((r, \theta)\) の同時密度関数を求める。
\[\begin{equation}
\left\{\,
\begin{aligned}
X = r \cos{\theta} \\
Y = r \sin{\theta}
\end{aligned}
\right .
\end{equation}\]
すると、ヤコビ行列とヤコビアンをこんな感じで計算ができる。
\[\begin{equation}
% ヤコビ行列
\left(
\begin{matrix}
\frac{\partial{x}}{\partial{r}} & \frac{\partial{x}}{\partial{\theta}} \\
\frac{\partial{y}}{\partial{r}} & \frac{\partial{y}}{\partial{\theta}}
\end{matrix}
\right)
=
\left(
\begin{matrix}
\cos{\theta} & -r\sin{\theta} \\
\sin{\theta} & r\cos{\theta}
\end{matrix}
\right) \\
\end{equation}\]
\[\begin{equation}
% ヤコビアン
|\det{J}| = r \cos^2{\theta} + r \sin^2{\theta} \\
= r(\cos^2{\theta} + \sin^2{\theta}) = r
\end{equation}\]
したがって、同時分布は
\[\begin{equation}
% rと\thetaの同時分布
f(r, \theta) = f_X(r \cos{\theta})f_Y(r \sin{\theta})r = r c^2 \exp{\{- \frac{r^2}{2}\}}
\end{equation}\] こいつを\(r, \theta\) について積分すると、実質\(r\) についての積分なので
\[
c^2 \int_0^{\infty} r \exp{\{- \frac{r^2}{2}\}} dr = 1
\]
これを解くと\(\frac{1}{\sqrt{2\pi}}\) になる。
多次元分布の期待値と分散、共分散
多次元確率分布の期待値はだいたい1次元と同じ。 \((X,Y)\) の実現値の関数を\(g(x,y)\) とおくと、特に離散の場合は以下。
\[
E(g(X, Y)) = \sum_{x \in X}\sum_{y \in Y} g(x,y)p(x, y)
\]
多次元確率分布になると現れる概念に共分散がある。\(\mu_X = E(X)\) 、\(\mu_Y = E(Y)\) とおくと、共分散\(Cov(X, Y)\) は以下のように定義される。
\[
Cov(X, Y) = \sigma_{X,Y} = E((X-\mu_X)(Y-\mu_Y))
\]
むしろこっちのほうが重要かもしれない。
\[\begin{equation}
\begin{aligned}
Cov(X,Y) = E((X - \mu_X)(Y - \mu_Y)) \\
= E(XY -X\mu_Y -Y\mu_X + \mu_X\mu_Y) \\
= E(XY) - E(X)E(Y) - E(X)E(Y) + E(X)E(Y)
= E(XY) - E(X)E(Y)
\end{aligned}
\end{equation}\]
相関係数はいわば「共分散の標準化」みたいなもん。
\[
Corr(X, Y) = \frac{\sigma_{X,Y}}{\sigma_X \sigma_Y} = \frac{Cov(X,Y)}{Var(X)Var(Y)}
\]
相関係数のとりうる範囲は-1~1までだが、証明ができる。\(X\) 、\(Y\) の平均からの偏差ベクトルを\(s_X = X-\mu_X\) 、\(s_Y = Y-\mu_Y\) とおく。\(s_X\) と\(s_Y\) との内積として表現できるし、分散はそれぞれのノルムとして表現できる。\(\theta\) とおくと、
\[\begin{equation}
\begin{aligned}
Cov(X,Y) = s_X \cdot s_Y \\
Var(X) = \|s_X\|\\
Var(Y) = \|s_Y\|\\
\Rightarrow Corr(X, Y) = \frac{s_X \cdot s_Y}{\|s_X\|\|s_Y\|} = \cos{\theta}
\end{aligned}
\end{equation}\]
余弦の定義から、\(-1 \leq \cos{\theta} \leq 1\) であるから、相関係数の値の範囲を証明できた。
実のところ、相関と因果が違うように、相関がないことと、その2変数が独立であることもまた違う。\(X\) 、\(Y\) が独立ならば、この2変数は無相関である」は証明できるが、\(X=Y^2\) を考えればよい。
\(E(XY) = E(X)E(Y)\)
確率変数の和の分散の公式、つまり確率変数\(X,Y\) を使って\(Z=X+Y\) なる変換をしたときのZの分散を考える。\(E(X+Y)=E(X)+E(Y)\) がどんなときにも成り立つ)
\[\begin{equation}
\begin{aligned}
Var(Z) = E[(Z-E[Z])^2] = E[Z^2-2ZE[Z] - E[Z]^2] \\
= E[(X+Y)^2 - 2(X+Y)E[X+Y] + E[X+Y]^2] \\
= E[(X-E[X]+Y-E[Y])^2] \\
= Var(X) + 2Cov(X,Y) + Var(Y)
\end{aligned}
\end{equation}\]
よって\(Var(X+Y) = Var(X) + Var(Y)\) が成り立つのは、\(X,Y\) が独立なときに限る。\[
Var(X_1+X_2+\dots+X_b) = \sum_{i=1}^n Var(X_i)
\]
期待値行列と分散共分散行列
ここは「このように書く」という話。 \(\textbf{X} = (X_1, X_2, \dots, X_n)^T\) を確率変数ベクトルといい、\(E[\textbf{X}] = (E[X_1],E[X_2],\dots,E[X_n])^T\) を期待値ベクトルとして定義する。
この確率ベクトルの分散\(Var(X_i)\) と、\(X_i,X_j\) の共分散を\(\sigma_{i,j}\) としたときに、\(n\) 次正方行列
\[\begin{equation}
\left(
\begin{matrix}
Var(X_1) & \sigma_{1,2} & \dots & \sigma{1, n} \\
\vdots & \vdots & \ddots & \vdots \\
\sigma_{n, 1} & \sigma_{n,2} & \dots & Var(X_n)
\end{matrix}
\right)
\end{equation}\]
を分散共分散行列という
多次元確率分布の母関数
「このように書く」ということになっているので省略。
分布の加法性
有名どころで、証明も難しくないので、省略。
回帰分析と条件付き期待値、条件付き分散
条件付き期待値は、条件付き分布を使った\(y\) の期待値。 \[
E[Y|X] = E[Y | X = x] = \int_{-\infty}^{\infty} yf_{Y|X=x}(y)dy
\]
条件付き期待値は、\(E[Y]\) が存在するならほとんどすべての\(x\) に対して\(E[Y|X=x]\) が存在する。\(g(X, Y)\) に対し、\(X=x\) が与えられたときの条件付き期待値 \[
E[g(X, Y)|X] = E[g(X, Y) | X = x] = \int_{-\infty}^{\infty} g(x,y)f_{Y|X=x}(y)dy
\]
条件付き期待値の面白い動きは\(X\) をいろいろに変えたときの関数\(h(x)=E[Y|X=x]\) として考えることができるし、発展して\(X\) の分布を考えることで\(h(x)\) を確率変数と捉えることも可能。
このとき「全確率の公式」あるいは「繰り返し期待値の公式」として、いかが成り立つ \[
E[h(X)] = E[E[Y|X]]のとき、E[Y] = E[E[Y|X]]
\]
\[\begin{equation}
\begin{aligned}
E[Y] = \int \int yf(x,y)dydx = \int (\int{y\frac{f(x,y)}{f_X(x)}}dy)f_X(x)dx \\
= \int{E[Y|X]f_X(x)} dx
\end{aligned}
\end{equation}\]
ここで\(f_{Y|X}(y) = \frac{f(x,y)}{f_X(x)}\) のハズ。条件付き分布の定義から。
条件付き分散は以下。
\[
Var(Y|X) = E[(Y-E[Y|X])^2 | X]
\]
詳細は本誌を見てほしいが、Yの分散が「Yの条件付き分散の期待値」と「Yの条件付き期待値の分散」に分解されるという以下の性質は重要。なぜなら2.13や2.14でこれを使うので。
\[
Var(Y) = E[Var(Y|X)]+Var(E[Y|X])
\]
これはYを目的変数とおいたときに、その分散を(特にパラメータのない)Xで説明しようとするモデルなので、実質分散分析に近い。
より一般化して、\(X\) をn次元確率変数ベクトルとし、それの何らかの変換\(g(X)\) で、別の確率変数\(Y\) の振る舞いを予測する。うまく\(g(x)\) の形を選んで、\(Y\) と似たふるまいを実現したい。
\[
MSPE = E[(Y - g(x))^2]
\]
このMSPEを最小にするような\(g(x)\) を求めたい。この条件を満たすような\(g(X)\) はE[P(Y|X)]に一致する。また、MSPEの最小値は条件付き分散の期待値に一致する。 つまり、\(g^*(X) = E[Y|X=x]\) とおくと、
\[
E^X[Var[Y|X]] = E[(Y - g^*(x))^2] \leq E[(Y - g(X))^2]
\]
が、任意の\(g(x)\) で成り立つ。証明は本誌を参照すること。
条件付き期待値は、平均自乗予測誤差に対して良い「予測量」を与える。ここで、予測量とは\(\hat{Y}\) など、目的変数を予測するための関数を指す。特に
\[
g(x) = a + b_1X_1 + b_2X_2 + \dots + b_nX_n
\]
という形で特定化した場合に「最良線形予測量」と呼ぶ。\(g(x) = a + \sum_{i = 1}^nb_iX_i\) とおいて考え直す。 以下は3.64式までを整理したつもりだが、最小二乗法によって、最小化したい関数は、\(X\) で説明できるかという問題に置き換わる。
\[\begin{equation}
\begin{aligned}
E[(Y - g(x))^2] = E[(Y - (a + \sum_{i = 1}^nb_iX_i))^2] \\
\Rightarrow a = E[Y] - (\sum_{i = 1}^nb_iE[X_i]), \\
Var[Y]-2\sum_{i = 1}^nb_iCov[Y, X_i] + \sum_{i, j}^nb_ib_jCov[X_i, X_j]
\end{aligned}
\end{equation}\]
最終的に、説明変数の分散共分散行列\(\Sigma_{XX}\) が正則であるという条件下で、\(b\) が\(\Sigma_{XX}^{-1}\sigma_{XY}\) で表現できる。
条件付き期待値は、あらゆる\(X\) の関数の中で最も良い予測量を与えるので、